ハフマン符号
ハフマン符号(Haffman Coding) は、デビット・ハフマンによって開発された符号で、データの可逆圧縮に利用されます。出現頻度の高いデータに短いビット列を、逆に出現頻度の低いデータに長いビット列を割り当てることで、データ全体でのデータ量の削減を実現します。
ハフマン符号のアルゴリズムは古典的(代表的)な圧縮アルゴリズムであり、ZIPやJPEGといった圧縮フォーマットでも利用されています。
ハフマン符号でデータの符号化(圧縮)を行う場合、出現頻度を知るために全データを一度調べてから、符号の割当を行う必要があります。その後全データを先頭から対応する符号に置き換えていくことになるので、計2回のデータ走査が必要になります。このデータを2回走査し、静的な符号に変換するアルゴリズムを、静的ハフマン符号といいます。このページで「ハフマン符号」として紹介するのはこのアルゴリズムです。
上記の2回データを走査する方法は、データサイズが大きくなると処理効率の面で問題が生じる可能性があります。この問題を解消するために、出現頻度を調べながら、動的に符号を割り当てていく適応型ハフマン符号というアルゴリズムも存在します。
特徴
可変長符号
ハフマン符号は可変長符号です。例えばASCIIコードは 8bit(1byte) の固定長符号として扱われます。
"A", "B", "C", "D", "E" の5文字から構成される文字列 "AAAAAABBBBCCCDE" について考えてみます。通常のASCIIコードでは5文字のデータは以下のように符号化されます。
| 文字 | 符号(10進数) |
|---|---|
| A | 1000001 (65) |
| B | 1000010 (66) |
| C | 1000011 (67) |
| D | 1000100 (68) |
| E | 1000101 (69) |
15文字の文字列なので 15*8bit なので 15byte のデータ量となります。 1文字あたり 8bit のデータを割り振る ASCIIコード では全256文字表現できます。ただしこの文字列に限って言えば、出現する文字種類はたった5種類です。したがって、1文字あたり 3bit あれば全データを表現することができます。例えば以下の表のようにです。これで 15*3bit なので 45bit になります。
| 文字 | 符号 |
|---|---|
| A | 001 |
| B | 010 |
| C | 011 |
| D | 100 |
| E | 101 |
この時点でいくらかのデータ圧縮がなされていますが、そもそも出現する文字種類にも出現頻度(回数)に偏りがあることが分かります。したがって、よく出現するデータにより短いビット列を、あまり出現しないデータには逆に長いビット列を割り当てることでさらにデータ量圧縮を図ります。
以下はハフマン符号の表です。
| 文字 | 符号 | 出現回数 |
|---|---|---|
| A | 0 | 6 |
| B | 10 | 4 |
| C | 111 | 3 |
| D | 1100 | 1 |
| E | 1101 | 1 |
この割り当てた符号をハフマン符号といいます。割り当ての規則は後述しますが、もっともよく出現する "A" に最短となる 1bit の符号を割り当てています。この割り当てでのデータサイズは
6*1bit + 4*2bit + 3*3bit + 1*4bit + 1*4bit = 29bit
となり、固定長での割り当て(45bit)よりさらに圧縮されていることが確認できます。さらにハフマン符号は、元の符号より必ず短くかつ常に最適(最短)の割り当てがなされることが証明されています。
接頭符号
ハフマン符号は接頭符号呼ばれる符号です。接頭符号は任意の符号が、ほかの符号の接頭部にならないような符号のことです。例えば "0", "1", "01" となる可変長符号がある場合、符号 "0" が 符号 "01" の接頭部分に当てはまるので接頭符号とは言えません。すでに上で示したハフマン符号の表を確認してもらえると、どの文字に対応する符号も、他の符号の接頭部分に対応していないことが分かります。
可変長符号が接頭符号であるということは、一意複合可能と 瞬時復号可能という2つの性質を与えてくれます。
一意複合可能とは、ある圧縮されたデータを複合する際に複合結果が一意に定まるということです。例えば "0", "1", "01" となる可変長符号で構成されるデータ "01" を復号する場合、"0 1" となるか、"01" となるか一意に決めることができません。符号化に一意複合可能なことは必須の要件です。
瞬時復号可能とは、ある圧縮されたデータがビット列として与えられた場合に、各符号の最後のビットが読み込まれた時点でその符号を確定できるというような性質です。ビット列を最後まで読まなくても先頭から順に復号していくことができるという意味で、瞬時復号可能といいます。瞬時復号可能ではない符号では、複合処理が複雑になり効率性に影響してしまいます。
符号化アルゴリズム
ハフマン木と符号化
ハフマン符号を得るためには、ハフマン木という2分木を作成する必要があります。生成したハフマン木をたどることで符号化を行います。以下その手順です。
- ハフマン木のノードを保持するリスト(Q)を生成します。
- データ種類と出現回数を持つ葉ノードを生成し、リスト(Q)に追加します。
-
節ノード(N)を生成しQに追加します。
- Qから最小の出現回数を持つノード(R)を取り出します。
- Qから最小の出現回数を持つノード(L)を取り出します。
- Nの左の子ノードにLを、Nの右の子ノードをにRを、出現回数に左右の子ノードの持つ出現回数の和を設定します。
- 3. の手順をQの個数が1になるまで繰り返します。
- Qに残ったノードがハフマン木のルートノードになります。
ハフマン木のノードが子ノードを保つ場合、必ず左右に子ノードを持ちます。更にルートノードのみで子ノードを持たないのは許されません。したがって、データが1種類のみしか出現しない場合には別で制御しなければなりません。ダミーのルートノードを用意し、その左右の子ノードにルートをもたせておけばよいでしょう。
リスト(Q)は最小値が取り出せればよい(ソートされてなくてもよい)ので、2分ヒープを使うと効率的です。
ファイルの圧縮を行う場合、ファイルのデータをバイト単位で出現回数を調べますが、わかりやすくここでは文字列の符号化を考えます。いずれも 1byte 単位なので同じように考えられます。
"A", "B", "C" の3文字から構成される文字列 "AAAABBC" の符号化を行うと以下のようなハフマンツリーが得られます。
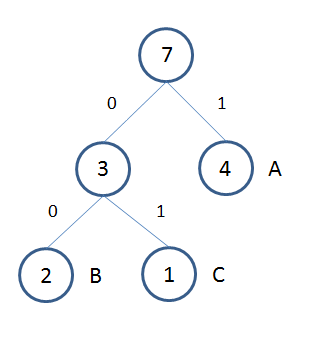
ハフマン木からそれぞれのデータに対応する符号を得るのは簡単です。ルートノードから目的のデータが格納されている葉ノードに向かい左のノードに進む場合は "0" 右のノードに進む場合は "1" をとることで、対応する符号が得られます。上の例だと "A" は右なので "1" 、"B" は左右なので "01"、"C" は左左なので "00" がそれぞれ符号が割り振られるといった仕組みです。
重要なハフマン符号のアルゴリズムは以上です。ただし実際にファイルをこのアルゴリズムのみで圧縮・復号するには、更に以下事項も考えなければなりません。
ハフマン木自体の符号化
ここまでの手順でわかるのは、圧縮データを復号する際にもハフマン木が必要になります。つまり、圧縮データには、圧縮に使用したハフマン木自体の情報も入れなければ行けません。ハフマン符号 + ハフマン木自体のデータ が圧縮されたデータということになります。
ハフマン木の作成にはデータの種類と出現頻度(回数)を必要とします。したがってそれらすべてを記録保持しておく方法が考えられます。しかしそれよりも単純に木構造自体をビット列化してしまう方が、短いデータ量で表現できるので、その方法をまとめます。
ハフマン木自体をビット列化するのは、手順としては以下のように行います。
-
ハフマン木を深さ優先で探索します。(左の子ノード優先)
- 探索しているノードが節ノードの場合、0を出力します。
- 探索しているノードが葉ノードの場合、1を出力し、対象データ8bitを出力します。
上のハフマン木をビット列化すると、"0 0 1 X 1 Y 1 Z" となります。X, Y, Zには対応するデータ8bit分が出力されると考えてください。
ちなみにこの手法で生成されるデータは可変長ですが、瞬時復号可能なので問題ありません。右の子ノードが葉ノードのタイミングでハフマン木の再構成が完了します。
圧縮データの構成
ハフマン符号は可変長符号のため、復号の際に何byte分出力して完了なのかを知っておく必要があります。したがって元データのファイルサイズもデータの先頭に保持することにします。よって圧縮データの構成は、
ファイルサイズ(4byte) + ハフマン木自体のビット列 + 符号化されたデータ
とします。ハフマン木も符号化されたデータも可変長のデータです。
圧縮率
圧縮率についての細かい数学的な話はしませんが、圧縮率はデータの偏り具合によってはうまく圧縮できません。例えば完全にランダムなデータ(すべてのデータ出現回数が等しいなど)については、全く圧縮できなかったりします。
サンプルコード
圧縮はそれなりの速度でできますが、復号が結構時間がかかります。環境にもよるのですが、うまく高速化できる方法があれば誰か教えてください。ファイルだけでなく、ASCII文字列データの圧縮もできるようにしてます。
使い方は簡単です。Haffmanクラスを生成し、Encode(Decode)メソッドにファイル名を渡します。文字列で試す場合は、DebugStringメソッドに文字列を渡します。
C#
using System;
using System.Collections.Generic;
using System.IO;
using System.Linq;
using System.Text;
public class Haffman
{
// バイトごとの出現回数を計算
private int[] GetFrequency(byte[] bytes)
{
var freq = Enumerable.Repeat(0, 256).ToArray();
foreach (var b in bytes)
{
freq[b]++;
}
return freq;
}
// ハフマンツリー生成
private HaffmanNode GenerateHaffmanTree(int[] freq)
{
var nodeList = new List<HaffmanNode>();
for (int i = 0; i < 256; i++)
{
if (freq[i] == 0) continue;
var node = new HaffmanNode((byte)i, freq[i]);
nodeList.Add(node);
}
// 残り1つになるまで処理をする
while (nodeList.Count > 1)
{
// 先頭に最小値が来るようにソートする
// ソートではなく2分ヒープを使うほうが効率的
nodeList = nodeList.OrderBy(e => e.Frequency).ToList();
// 出現頻度が最小値のノード2つを取り出す
var left = nodeList[0];
var right = nodeList[1];
nodeList.RemoveAt(0);
nodeList.RemoveAt(0);
// 左右の出現頻度の和を持つノードを生成しキューに追加
var node = new HaffmanNode(left, right);
nodeList.Add(node);
}
// キューに残っているノードがハフマンツリーのルートノード
var root = nodeList[0];
// 1種類のデータしか出現しない場合はダミーノードを用意
if (root.IsLeaf)
{
var dummyRoot = new HaffmanNode();
dummyRoot.IsLeaf = false;
dummyRoot.Left = root;
dummyRoot.Right = root; // 左右にノードが必要なので
return dummyRoot;
}
return root;
}
// 圧縮用ハフマンコード表生成
private Dictionary<byte, bool[]> GetHaffmanCodeTable(HaffmanNode node)
{
var dict = new Dictionary<byte, bool[]>();
for (int i = 0; i < 256; i++)
{
var b = (byte)i;
dict[b] = GenerateHaffmanCode(node, b);
}
return dict;
}
// 指定データについてのハフマンコード生成
private bool[] GenerateHaffmanCode(HaffmanNode node, byte symbol, List<bool> bits = null)
{
if (bits == null) bits = new List<bool>();
if (node.IsLeaf && (node.Value == symbol))
{
// 葉ノードでデータが一致する場合
return bits.ToArray();
}
if (node.Left != null)
{
// 左の子ノードがある場合、false(0) を追加して再帰呼び出し
bits.Add(false);
var result = GenerateHaffmanCode(node.Left, symbol, bits);
if (result != null) return result;
// 左の子ノードに見つからなかった場合、追加したデータを取消
bits.RemoveAt(bits.Count - 1);
}
if (node.Right != null)
{
// 右の子ノードがある場合、true(1) を追加して再帰呼び出し
bits.Add(true);
var result = GenerateHaffmanCode(node.Right, symbol, bits);
if (result != null) return result;
// 右の子ノードに見つからなかった場合、追加したデータを取消
bits.RemoveAt(bits.Count - 1);
}
return null; // 葉ノードで見つからなかった場合
}
// ハフマンツリー自体をビット化
private bool[] ConvertHaffmanTreeToBits(HaffmanNode root)
{
var bits = new List<bool>();
// スタックを使って深さ優先探索
var stack = new Stack<HaffmanNode>();
stack.Push(root);
while (stack.Count > 0)
{
var node = stack.Pop();
if (node.IsLeaf)
{
// 葉ノードは true 出力
bits.Add(true);
// 実データ 8bit 出力
for (int i = 0; i < 8; i++)
{
bits.Add((node.Value >> 7 - i & 1) == 1);
}
}
else
{
// 葉ノードではないので false 出力
bits.Add(false);
// 左から優先的に走査したいので右から積む
if (node.Right != null) stack.Push(node.Right);
if (node.Left != null) stack.Push(node.Left);
}
}
return bits.ToArray();
}
// ハフマンツリーを再構成
private HaffmanNode RegenerateHaffmanTree(ref IEnumerable<bool> bits)
{
if (bits.First())
{
var symbol = bits.Skip(1).BitsToByte();
bits = bits.Skip(9); // 葉ノードフラグとデータ分読み飛ばし
return new HaffmanNode() { Value = symbol, IsLeaf = true };
}
else
{
bits = bits.Skip(1); // 葉ノードフラグ読み飛ばし
var left = RegenerateHaffmanTree(ref bits);
var right = RegenerateHaffmanTree(ref bits);
return new HaffmanNode(left, right);
}
}
// 圧縮
public void Encode(string inputFile, string outputFile)
{
// ファイル読み込み
var inputBytes = File.ReadAllBytes(inputFile);
// 出現回数(頻度)を計算
var freq = GetFrequency(inputBytes);
// ハフマンツリー生成
var root = GenerateHaffmanTree(freq);
DebugHaffmanTree(root, 0, "");
// ハフマンコード表生成
var haffmanDict = GetHaffmanCodeTable(root);
DebugHaffmanTable(haffmanDict);
// 書き込み対象のファイル
using (var writer = new BinaryWriter(File.OpenWrite(outputFile)))
{
// 圧縮前のファイルサイズ(バイト単位)出力
var size = BitConverter.GetBytes(inputBytes.Count());
writer.Write(size);
// ハフマンツリー自体をビット化(連結のための型にキャスト)
IEnumerable<bool> treeBits = ConvertHaffmanTreeToBits(root);
// ハフマン符号化したデータ
var haffmanCodes = inputBytes.Select(b =>
{
return haffmanDict[b];
});
// 書き込む全ビットデータからバイトデータ取得
var allByte = GetAllBytes(treeBits.ToArray(), haffmanCodes);
//writer.Write(allByte.ToArray());
foreach (var bt in allByte)
{
writer.Write(bt); // 1Byte毎の書き込みの方が速かった
}
}
}
// すべてのビットデータとして列挙
private IEnumerable<byte> GetAllBytes(bool[] treeBits, IEnumerable<bool[]> codes)
{
int i = 0;
byte result = 0;
foreach (var bit in treeBits)
{
// 指定桁数について1を立てる
if (bit) result |= (byte)(1 << 7 - i);
if (i == 7)
{
// 1バイト分で出力しビットカウント初期化
yield return result;
i = 0;
result = 0;
}
else
{
i++;
}
}
foreach (var bits in codes)
{
foreach (var bit in bits)
{
// 指定桁数について1を立てる
if (bit) result |= (byte)(1 << 7 - i);
if (i == 7)
{
// 1バイト分で出力しビットカウント初期化
yield return result;
i = 0;
result = 0;
}
else
{
i++;
}
}
}
// 8ビットに足りない部分も出力
if (i != 0) yield return result;
}
// 復号
public void Decode(string inputFile, string outputFile)
{
// ファイル読み込む(4バイト分とばしてビット化)
var inputBytes = File.ReadAllBytes(inputFile);
var bits = inputBytes.Skip(4).BytesToBits();
// 圧縮前ファイルサイズ
int size = BitConverter.ToInt32(inputBytes.Take(4).ToArray(), 0);
// ハフマンツリーの再構成
var root = RegenerateHaffmanTree(ref bits);
//DebugHaffmanTree(root, 0, "");
// 圧縮前のファイルサイズ分バイトデータ書き込み
using (var writer = new BinaryWriter(File.OpenWrite(outputFile)))
{
int counter = 0;
var node = root;
foreach (var bit in bits.ToArray())
{
if (node.IsLeaf)
{
// 見つかったらデータを出力し、ルートに戻す
writer.Write(node.Value);
counter++;
node = root;
if (counter >= size) break;
}
if (!node.IsLeaf)
{
// 葉ノードに到達するまで探す
if (bit == true)
node = node.Right;
else
node = node.Left;
}
}
}
}
// 動作確認用処理
private void DebugHaffmanTable(Dictionary<byte, bool[]> table)
{
Console.WriteLine();
Console.WriteLine($"DebugHaffmanTable");
for (int i = 0; i < 256; i++)
{
if (table[(byte)i] != null)
{
var code = table[(byte)i].Select(b => b ? '1' : '0').ToArray();
Console.WriteLine($"{i.ToString("X2")}: {new string(code)}");
}
}
}
private void DebugHaffmanTree(HaffmanNode node, int indent, string bitCode)
{
if (indent == 0)
{
Console.WriteLine();
Console.WriteLine("DebugHaffmanTree");
}
var bits = new List<bool>();
bits.AddRange(bits);
int indent_ = indent > 0 ? indent - 1 : 0;
var indentStr = new string(' ', 2 * indent_) + " --";
if (node.IsLeaf)
{
Console.WriteLine(indentStr + $"{node.Value.ToString("X2")}({bitCode})");
}
else
{
Console.WriteLine(indentStr + $"");
if (node.Left != null)
{
DebugHaffmanTree(node.Left, indent + 1, bitCode + "0");
}
if (node.Right != null)
{
DebugHaffmanTree(node.Right, indent + 1, bitCode + "1");
}
}
}
public void DebugString(string str)
{
var bytes = Encoding.ASCII.GetBytes(str);
var freq = GetFrequency(bytes);
var root = GenerateHaffmanTree(freq);
DebugHaffmanTree(root, 0, "");
var table = GetHaffmanCodeTable(root);
DebugHaffmanTable(table);
}
// ハフマンノードクラス
public class HaffmanNode
{
public bool IsLeaf { get; set; }
public byte Value { get; set; }
public int Frequency { get; set; }
public HaffmanNode Left { get; set; }
public HaffmanNode Right { get; set; }
// 末端のノードを生成するためのコンストラクタ
public HaffmanNode(byte value, int frequency)
{
// データと出現頻度を保持する
this.Value = value;
this.Frequency = frequency;
this.IsLeaf = true;
}
// 子ノードを持つ節を生成するためのコンストラクタ
public HaffmanNode(HaffmanNode left, HaffmanNode right)
{
this.Left = left;
this.Right = right;
this.Frequency = left.Frequency + right.Frequency;
this.IsLeaf = false;
}
public HaffmanNode() { }
}
}
public static class Extentions
{
// bool[] => byte
public static byte BitsToByte(this IEnumerable<bool> bits)
{
return bits.BitsToBytes().FirstOrDefault();
}
// bool[] => byte[]
public static IEnumerable<byte> BitsToBytes(this IEnumerable<bool> bits)
{
int i = 0;
byte result = 0;
foreach (var bit in bits)
{
// 指定桁数について1を立てる
if (bit) result |= (byte)(1 << 7 - i);
if (i == 7)
{
// 1バイト分で出力しビットカウント初期化
yield return result;
i = 0;
result = 0;
}
else
{
i++;
}
}
// 8ビットに足りない部分も出力
if (i != 0) yield return result;
}
// byte[] => bool[]
public static IEnumerable<bool> BytesToBits(this IEnumerable<byte> bytes)
{
foreach (var bt in bytes)
{
for (int i = 0; i < 8; i++)
{
yield return ((bt >> 7 - i) & 1) == 1;
}
}
}
}